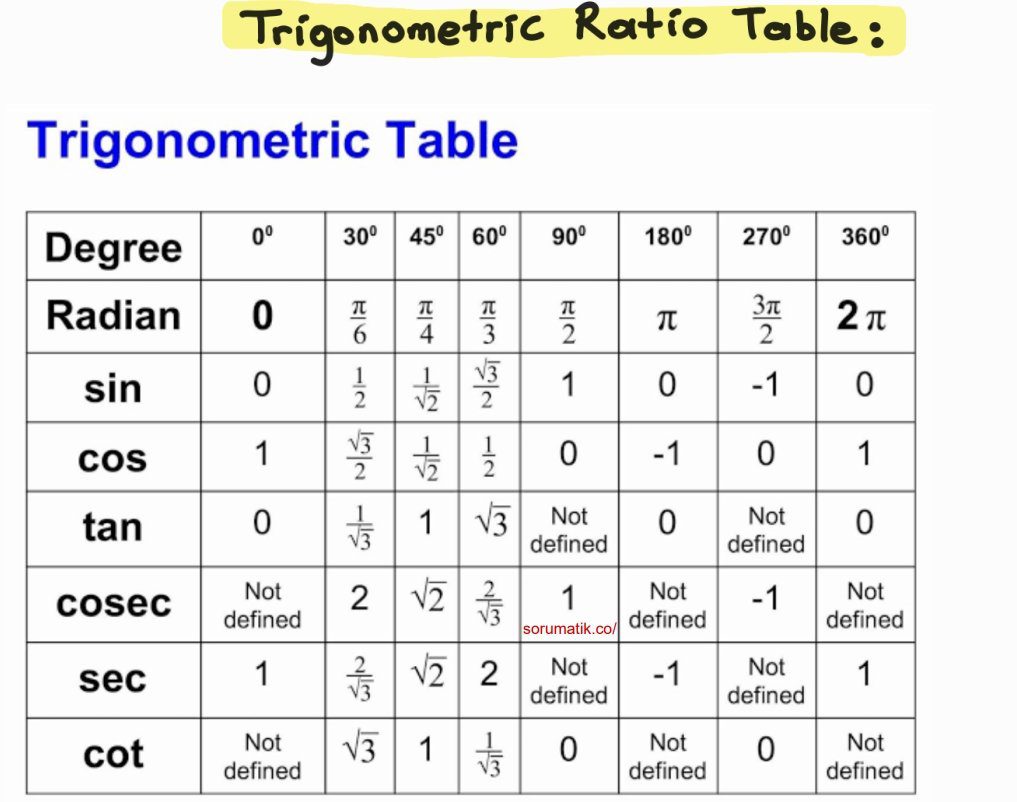
math formulas
List of Trigonometry Formulas PDF

Trigonometry formulas are a set of different formulas containing trigonometric identities used to solve problems based on the sides and angles of a right-angled triangle. In our article, we will list the trigonometry formulas. We will see trigonometric identities. You will also be able to download these formulas in PDF form.
List of Trigonometry Formulas
Basic Trigonometry Formulas
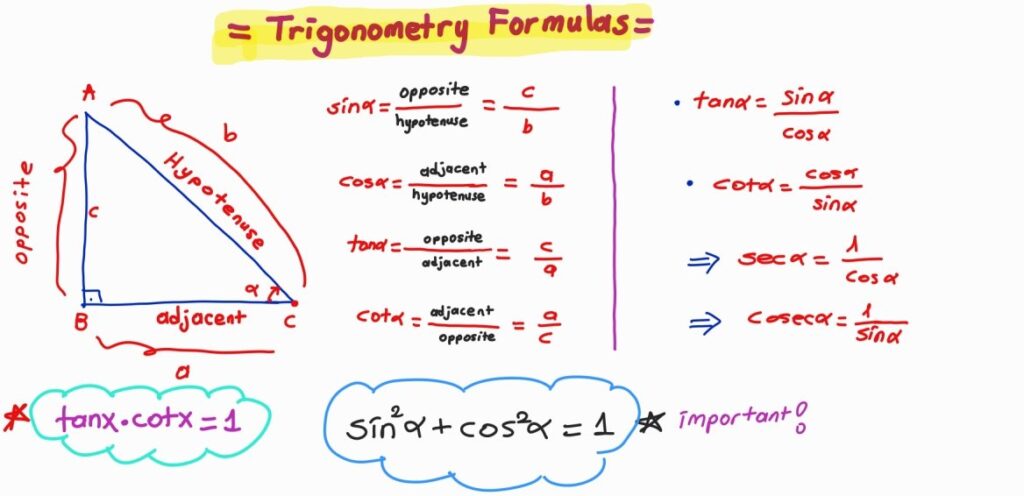
Trigonometric Ratio Formulas
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
Trigonometry Formulas Involving Reciprocal Identities
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
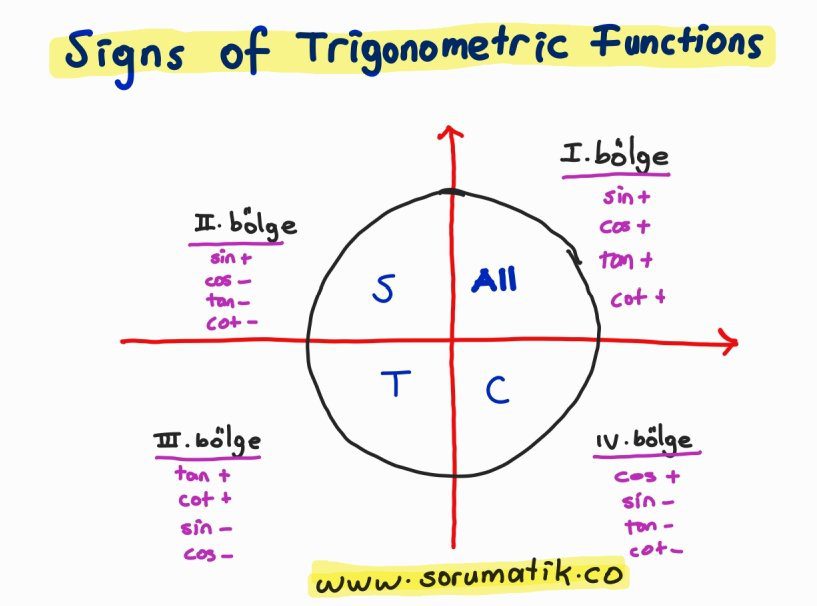
Signs of Trigonometric Functions
The Law of Sines
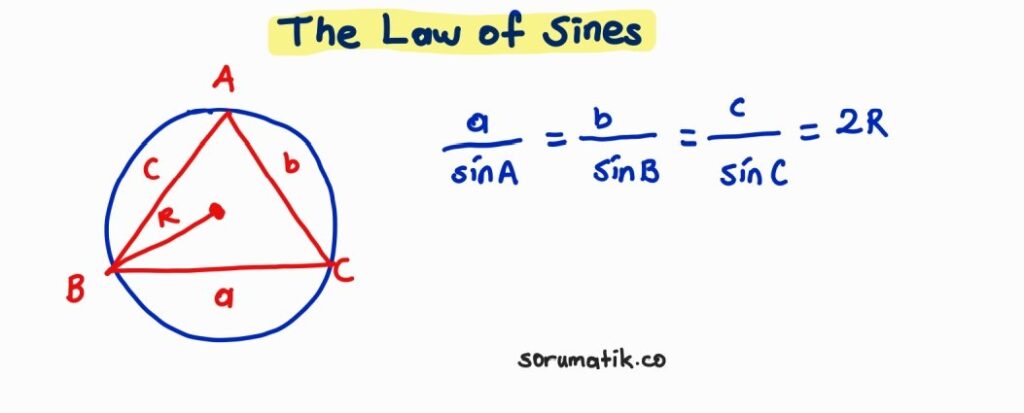
Sine Area Formula
(sin A)/a = (sin B)/b = (sin C)/c
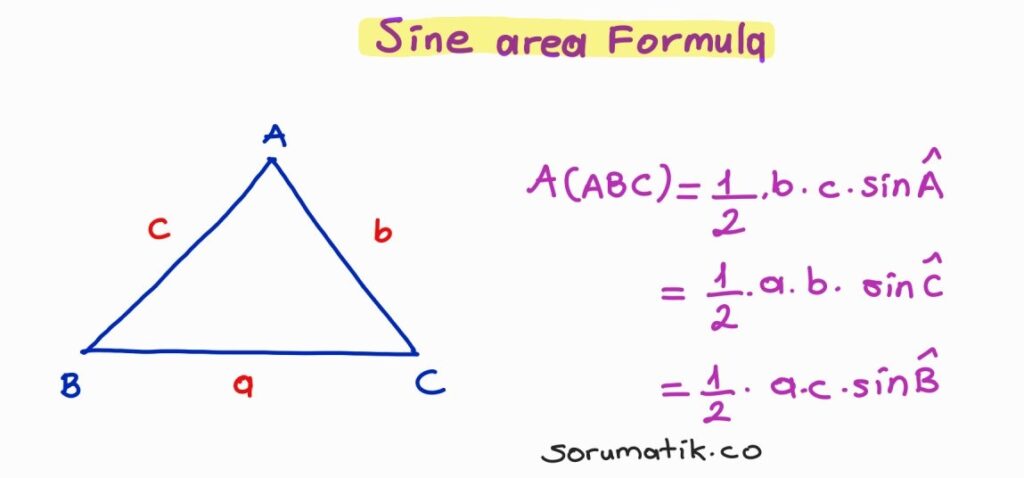
The Law of Cosines
- a2 = b2 + c2 – 2bc cosA
- b2 = a2 + c2 – 2ac cosB
- c2 = a2 + b2 – 2ab cosC

Trigonometry Formulas Involving Sum and Difference Identities

Trigonometry Formulas Involving Double Angle Identities
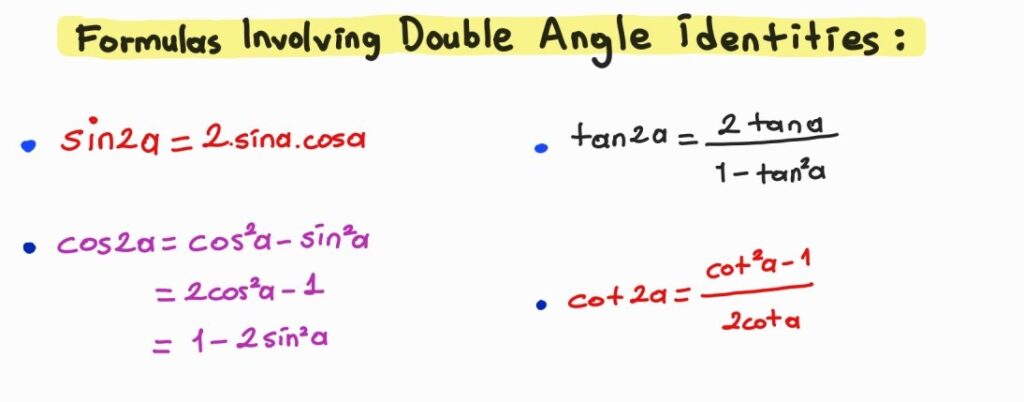
Trigonometry Formulas Involving Half-Angle Identities
sin (x/2) = ±√[(1 – cos x)/2]
cos (x/2) = ± √[(1 + cos x)/2]
tan (x/2) = ±√[(1 – cos x)/(1 + cos x)]
or, tan (x/2) = ±√[(1 – cos x)(1 – cos x)/(1 + cos x)(1 – cos x)]
tan (x/2) = ±√[(1 – cos x)2/(1 – cos2x)]
⇒ tan (x/2) = (1 – cos x)/sin x
Trigonometry Formulas Involving Sum to Product Identities
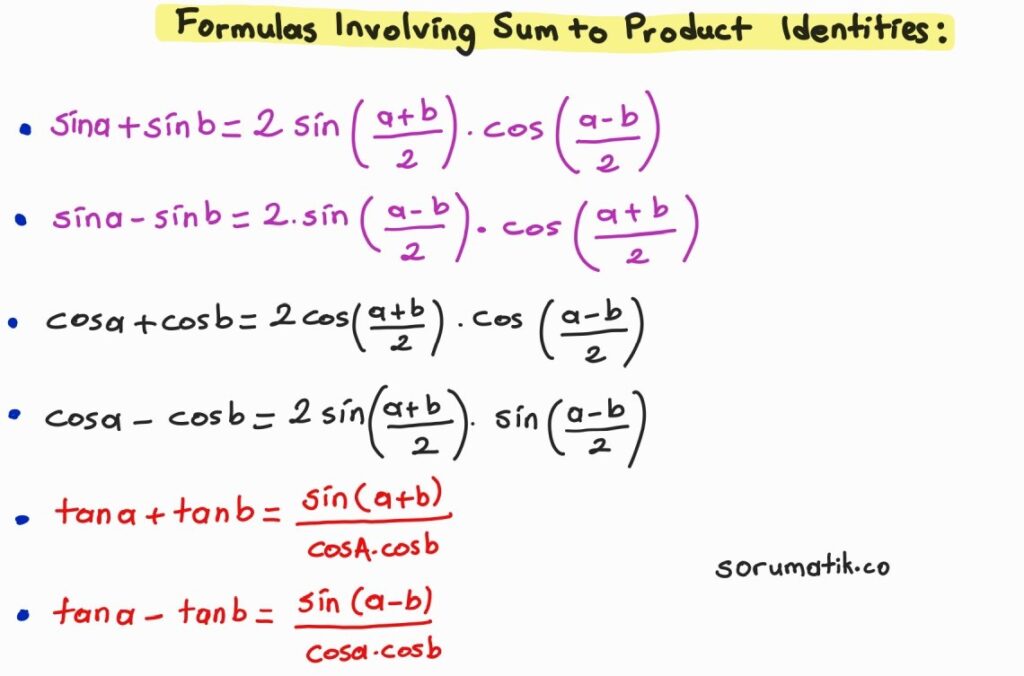
Trigonometry Formulas Involving Product Identities

Trigonometry Formulas Involving Periodic Identities(in Radians)
First Quadrant:
- sin (π/2 – θ) = cos θ
- cos (π/2 – θ) = sin θ
- sin (π/2 + θ) = cos θ
- cos (π/2 + θ) = – sin θ
Second Quadrant:
- sin (3π/2 – θ) = – cos θ
- cos (3π/2 – θ) = – sin θ
- sin (3π/2 + θ) = – cos θ
- cos (3π/2 + θ) = sin θ
Third Quadrant:
- sin (π – θ) = sin θ
- cos (π – θ) = – cos θ
- sin (π + θ) = – sin θ
- cos (π + θ) = – cos θ
Fourth Quadrant:
- sin (2π – θ) = – sin θ
- cos (2π – θ) = cos θ
- sin (2π + θ) = sin θ
- cos (2π + θ) = cos θ
Trigonometry Formulas Involving Co-function Identities(in Degrees)
- sin(90° − x) = cos x
- cos(90° − x) = sin x
- tan(90° − x) = cot x
- cot(90° − x) = tan x
- sec(90° − x) = cosec x
- cosec(90° − x) = sec x
Trigonometry Formulas Involving Reciprocal Identities
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
Inverse Trigonometry Formulas
- sin-1 (-x) = -sin-1 x
- cos-1 (-x) = π – cos-1 x
- tan-1 (-x) = -tan-1 x
- cosec-1 (-x) = -cosec-1 x
- sec-1 (-x) = π – sec-1 x
- cot-1 (-x) = π – cot-1 x
Trigonometry Formulas Involving Triple Angle Identities
- sin 3x = 3sin x – 4sin3x
- cos 3x = 4cos3x – 3cos x
- tan 3x = [3tanx – tan3x]/[1 – 3tan2x]