Trigonometri konusu matematik dersinin önemli konularından biridir. Bizlerde sizin için Trigonometri formülleri ve trigonometrik özdeşliklere PDF olarak yayınladık. AYT matematik dersinin konularından olan trigonometri konusu ile ilgili her yıl 4-5 soru sorulmaktadır. Sınav soru sayısının 40 soru olduğunu düşündüğümüzde bu sayı oldukça çoktur. Bu yüzden önemli bir konudur.
Tüm Trigonometri Formülleri PDF
Gelelim sizler için faydalı olacağını düşündüğümüz trigonometri formülleri yayınlamaya ! Bu yazımızda Trigonometrik Dik Üçgen Formülleri , Bölgelere Göre trigonometrik İşaret, Kosinüs Teoremi, Sinüs Teoremi, Sinüs Alan Formülü, Ters Trigonometrik Fonksiyonlar, Toplam Fark Formülleri, İki Kat Açı ve Yarım Açı Formülleri, Dönüşüm Formülleri, Ters Dönüşüm Formülleri, çift ve tek trigonomterik fonksiyonlar ve Trigonometrik değerler Tablosuna ulaşabilirsiniz. Yazı sonunda sayfanın alt bölümünde formülleri PDF olarak indirebilirsiniz.
Trigonometrik Fonksiyonlar
Trigonometri Dik Üçgen Formülleri:
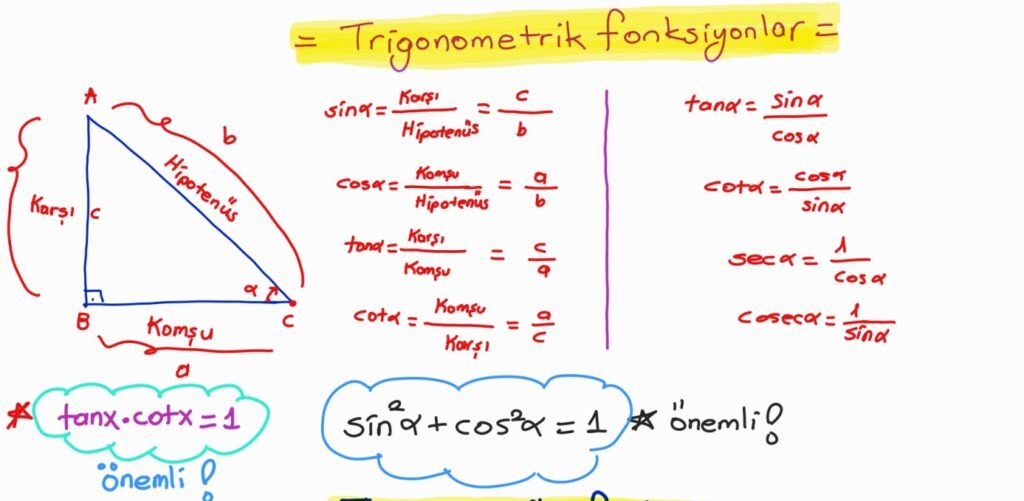
Trigonometri Bölgelere Göre İşaretler
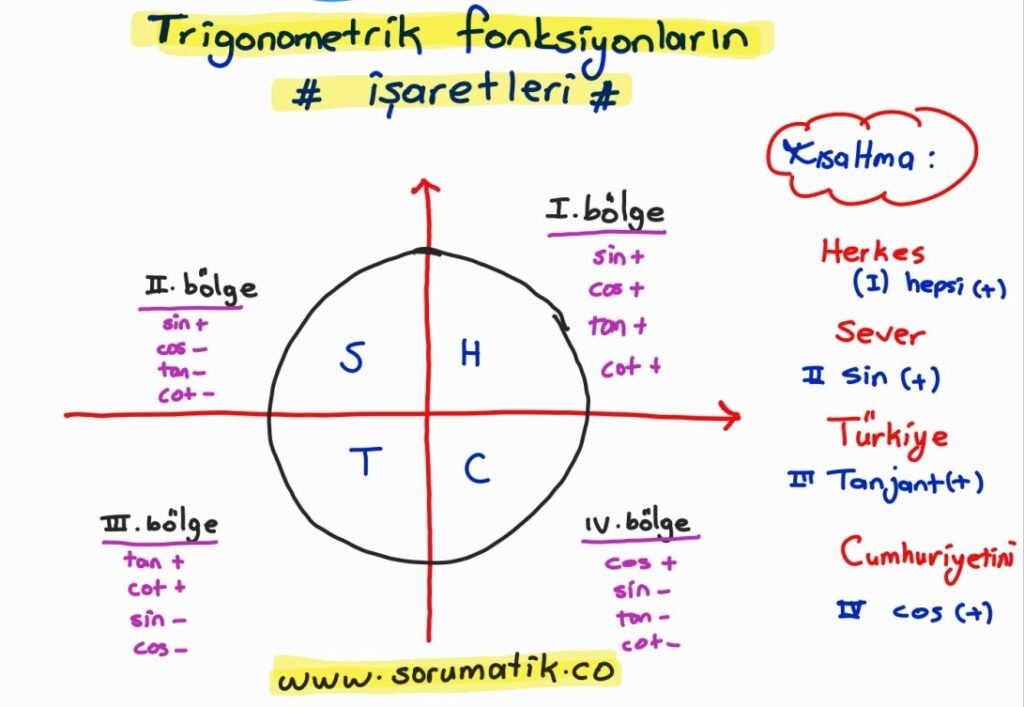
Sinüs Teoremi Formülü
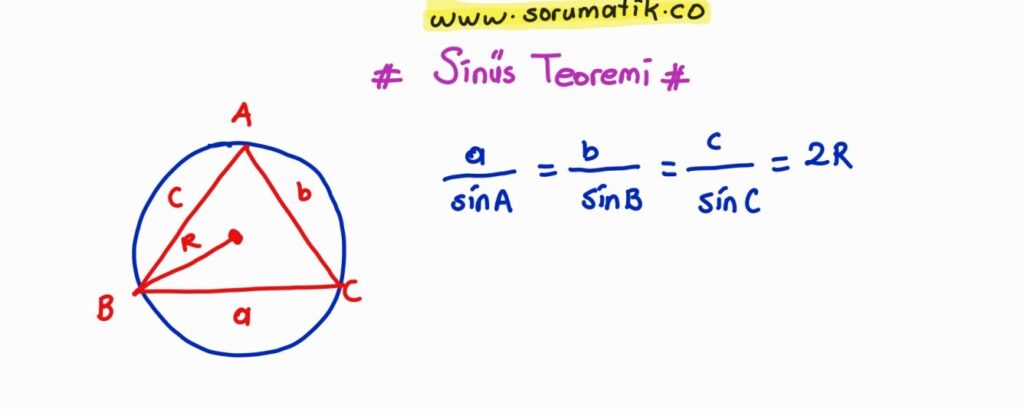
Sinüs Alan Formülü
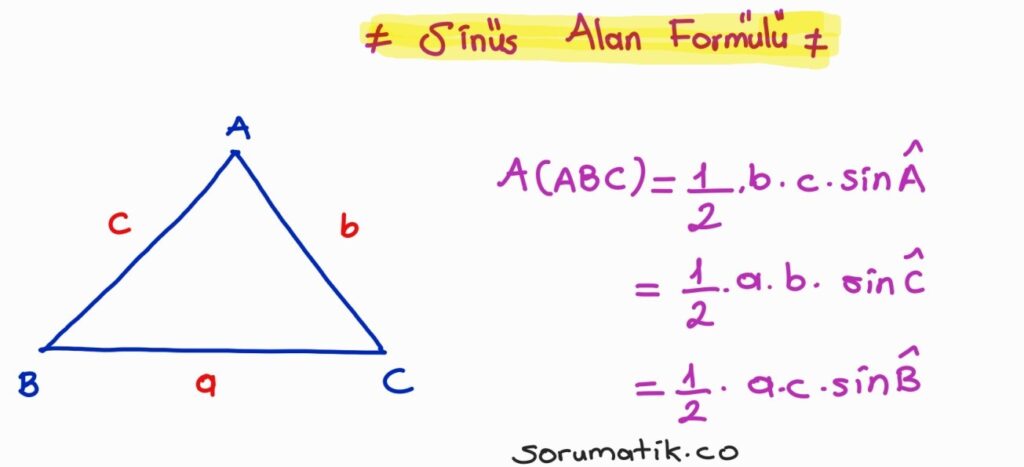
(sin A)/a = (sin B)/b = (sin C)/c
Kosinüs Teoremi Formülü
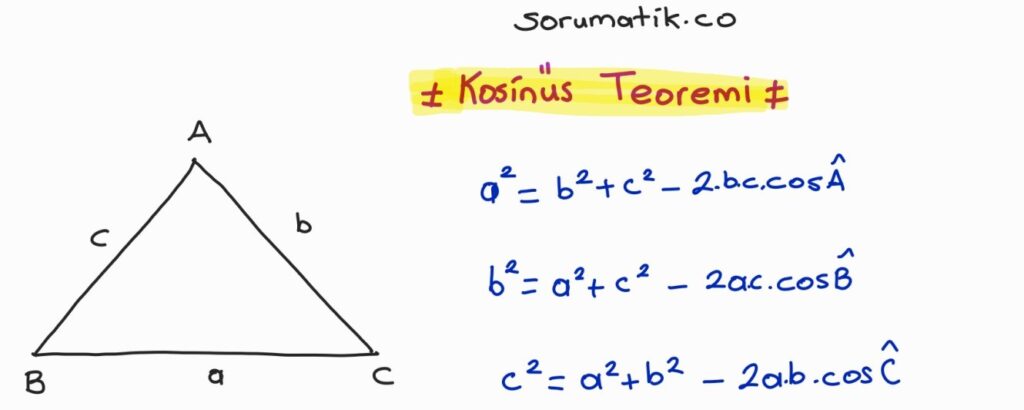
- a2 = b2 + c2 – 2bc cosA
- b2 = a2 + c2 – 2ac cosB
- c2 = a2 + b2 – 2ab cosC
Trigonometri Toplam-Fark Formülleri
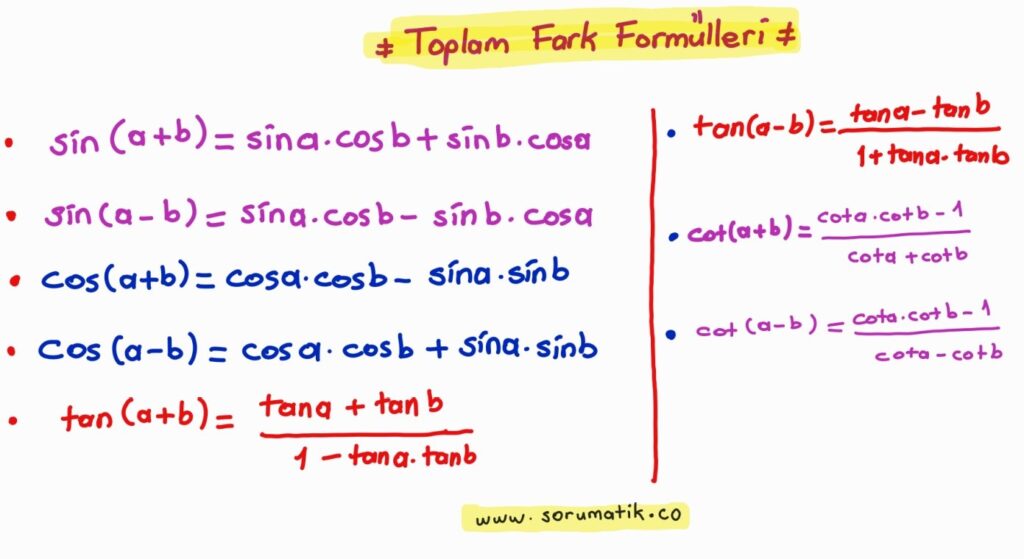
Düzeltme! Değerli okuyucular cot(a-b) yazarken üst kısımda pay bölümünde işaret dikkatimizden kaçarak yanlış yazılmıştır. Pay kısmı artı olmalıdır. cot(α-β) = (cot α . cot β + 1) / (cot β – cot α)
Trigonometri Yarım Açı Formülleri
Trigonometri Dönüşüm Formülleri
Trigonometri Ters Dönüşüm Formülleri
Trigonometrik Değerler Tablosu
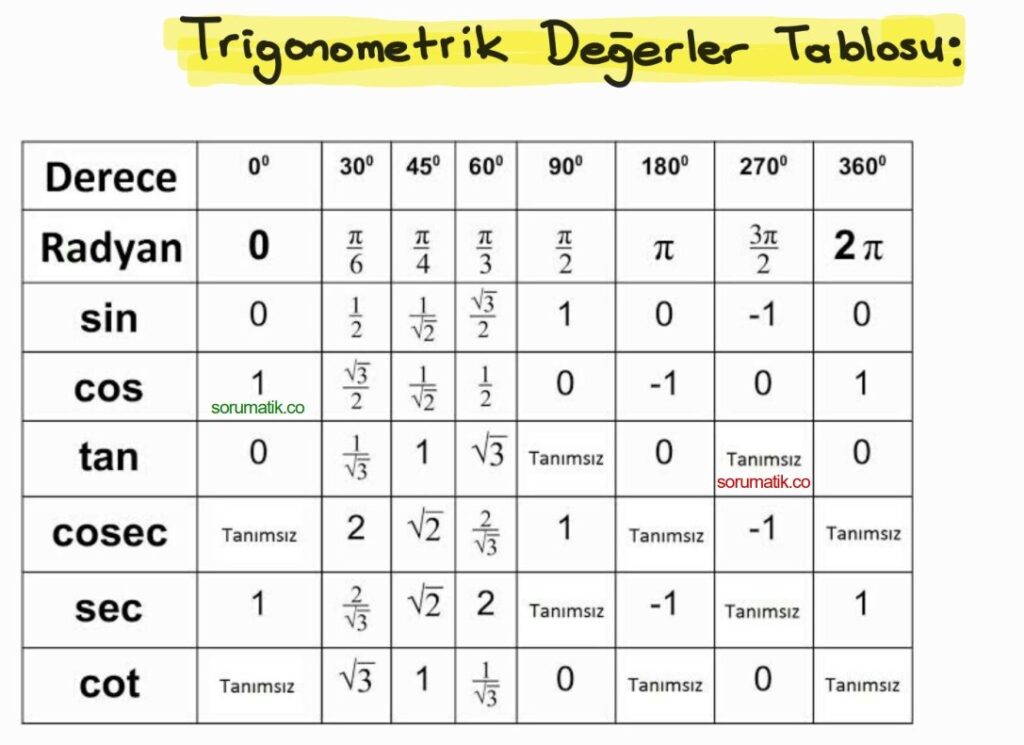
Tek ve Çift Trigonometrik Fonksiyonlar
Trigonometrik Fonksiyonların Eşitlikleri
- sin θ = Karşı/Hipotenüs
- cos θ = Komşu/Hipotenüs
- tan θ = karşı/komşu
- sec θ = Hipotenüs/komşu
- cosec θ = Hipotenüs/karşı
- cot θ = komşu/karşı
cosec-sec ve tan-cot fonksiyonlarının eşitlikleri
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
90 Derece ve Katları Şeklindeki Açıların Trigonometrik Oranları
1.Bölge:
- sin (π/2 – θ) = cos θ
- cos (π/2 – θ) = sin θ
- sin (π/2 + θ) = cos θ
- cos (π/2 + θ) = – sin θ
2.Bölge:
- sin (3π/2 – θ) = – cos θ
- cos (3π/2 – θ) = – sin θ
- sin (3π/2 + θ) = – cos θ
- cos (3π/2 + θ) = sin θ
3.Bölge:
- sin (π – θ) = sin θ
- cos (π – θ) = – cos θ
- sin (π + θ) = – sin θ
- cos (π + θ) = – cos θ
4.bölge:
- sin (2π – θ) = – sin θ
- cos (2π – θ) = cos θ
- sin (2π + θ) = sin θ
- cos (2π + θ) = cos θ
Birbirini doksan dereceye tamamlayan Açıların eşiti
- sin(90° − x) = cos x
- cos(90° − x) = sin x
- tan(90° − x) = cot x
- cot(90° − x) = tan x
- sec(90° − x) = cosec x
- cosec(90° − x) = sec x
Ters Trigonometrik Fonksiyonlar
- sin-1 (-x) = -sin-1 x
- cos-1 (-x) = π – cos-1 x
- tan-1 (-x) = -tan-1 x
- cosec-1 (-x) = -cosec-1 x
- sec-1 (-x) = π – sec-1 x
- cot-1 (-x) = π – cot-1 x
Sin3x, cos3x, tan3x eşiti
- sin 3x = 3sin x – 4sin3x
- cos 3x = 4cos3x – 3cos x
- tan 3x = [3tanx – tan3x]/[1 – 3tan2x]
Trigonometri Formüller PDF
Sizler için yayınladığımız Trigonometri formülleri PDF olarak indirmek için bağlantı linki: Trigonometrik formülleri PDF indir.
Elinize sağlık sonuna kadar okudum çok faydalı